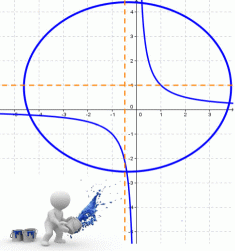
кривая задана уравнением y x 2 3 какая это кривая
5.2.8. Примеры решения задач по теме «Кривые 2-го порядка»
Определить тип уравнения кривой 2-го порядка:
Если L1·L2 > 0, то уравнение эллиптического типа;
Если L1·L2 0, следовательно, перед нами уравнение эллиптического типа.
В уравнении отсутствует произведение Ху, следовательно, квадратичная форма его старших членов имеет канонический вид; поэтому коэффициенты при Х2 и У2 являются собственными числами матрицы квадратичной формы. Итак, L1 = 4, L2 = 9, L1·L2 > 0, следовательно, перед нами уравнение эллиптического типа.
Геометрические образы, определяемые уравнением эллиптического типа:
— пустое множество («мнимый эллипс»).
Для приведения уравнения к каноническому виду нужно исключить из него слагаемые. Содержащие первые степени переменных. Для этого преобразуем левую часть:
Зададим параллельный перенос осей координат:
Тогда в новых координатах уравнение примет вид:
Каноническое уравнение эллипса.
Ответ: уравнение эллипса, канонический вид 
Привести уравнение к каноническому виду и указать геометрический образ, который оно определяет:
Собственные числа имеют разные знаки, значит, тип уравнения – гиперболический.
Геометрические образы, определяемые уравнением гиперболического типа:
— пара пересекающихся прямых.
Собственные числа имеют разные знаки, значит, тип уравнения – гиперболический.
Геометрические образы, определяемые уравнением гиперболического типа:
— пара пересекающихся прямых.
Заметим, что для данного уравнения нет необходимости искать явный вид преобразования координат, приводящего квадратичную форму к каноническому виду. Это связано с тем, что уравнение не содержит линейных членов, а его свободный член не изменится при преобразовании вида
Найденные собственные числа будут коэффициентами при Х2 и У2 для канонического вида квадратичной формы. Следовательно, в соответствующей координатной системе уравнение примет вид:
Каноническое уравнение гиперболы.
Ответ: уравнение гиперболического типа, канонический вид

Привести уравнение к каноническому виду и указать геометрический образ, который оно определяет:
Перед нами полное уравнение 2-го порядка, и для приведения его к каноническому виду потребуется провести оба преобразования координатных осей: поворот на такой угол, чтобы новые оси стали параллельными собственным векторам матрицы квадратичной формы (это преобразование квадратичной формы к каноническому виду), и параллельный перенос.
Перед нами полное уравнение 2-го порядка, и для приведения его к каноническому виду потребуется провести оба преобразования координатных осей: поворот на такой угол, чтобы новые оси стали параллельными собственным векторам матрицы квадратичной формы (это преобразование квадратичной формы к каноническому виду), и параллельный перенос.
Итак, тип уравнения – гиперболический.
Матрица перехода к новому базису:

Собственные векторы следует выбирать так, чтобы определитель матрицы перехода равнялся +1 – при этом не нарушается взаимное расположение координатных осей.
Запишем исходное уравнение в новых координатах:
2) Параллельный перенос:
В новых координатах получаем уравнение
Пара пересекающихся прямых.
Ответ: уравнение гиперболического типа, определяет пару пересекающихся прямых, канонический вид: У″ = ± 2Х″.
Не проводя преобразования координат, установить, что уравнение
Определяет прямую, и найти уравнение этой прямой.
Обратите внимание на то, что квадратичная форма, образованная старшими членами уравнения, является полным квадратом.
Иногда привести уравнение к простому виду удается с помощью алгебраических приемов. Представим левую часть уравнения в виде:
Ответ: уравнение определяет прямую Х – 3У + 2 = 0.
Эллипс, симметричный относительно осей координат, проходит через точки
Найти его эксцентриситет.
По условию задачи оси координат являются осями симметрии эллипса, поэтому, во-первых, его уравнение имеет канонический вид, а во-вторых, полуось А равна абсциссе точки А.
По условию задачи оси координат являются осями симметрии эллипса, поэтому, во-первых, его уравнение имеет канонический вид:
А во-вторых, полуось А равна абсциссе точки А, т. е. А = 6. Найдем B, подставив в уравнение эллипса координаты точки М:
Итак, уравнение эллипса:
Тогда расстояние от фокуса до начала координат
Вычислим эксцентриситет эллипса:
Ответ: эксцентриситет
Найдите расстояние от точки М до прямой У + 6 = 0, т. е. длину малой полуоси эллипса. Центром симметрии эллипса будет точка О пересечения прямых F1F2 (Y + 6 = 0) и МО, проходящей через точку М перпендикулярно F1F2.
Найдем расстояние от точки М до прямой У + 6 = 0, т. е. длину малой полуоси эллипса. Нормальный вид уравнения данной прямой: -у – 6 = 0, тогда
Центром симметрии эллипса будет точка О пересечения прямых F1F2 (Y + 6 = 0) и МО, проходящей через точку М перпендикулярно F1F2.
Поскольку прямая F1F2 параллельна оси абсцисс, прямая МО параллельна оси ординат; следовательно, ее уравнение: Х = 3. Тогда координаты точки О:
С учетом расположения осей эллипса можно утверждать, что в системе координат, полученной параллельным переносом начала координат в точку
Уравнение эллипса имеет канонический вид:
Найдем А из условия, что
Подставим найденные значения А и B в уравнение эллипса:
Ответ: уравнение эллипса: Х2 + 2У2 – 6Х + 24У + 31 = 0.
Составить уравнения директрис гиперболы.
Приведите уравнение гиперболы к каноническому виду и составьте уравнения директрис в виде
Приведем уравнение гиперболы к каноническому виду:
Осями симметрии являются координатные оси, А = 3, B = 4. Тогда
Ответ: уравнения директрис:
Написать уравнение гиперболы, имеющей вершины в фокусах, а фокусы – в вершинах эллипса
Найдите вначале координаты вершин и фокусов эллипса, а затем определите коэффициенты А и B в каноническом уравнении гиперболы.
Координаты вершин гиперболы: (А; 0) и (-А; 0), координаты фокусов: (С; 0) и (–С; 0). Соответственно координаты вершин эллипса: (А1; 0) и (-А1; 0), координаты фокусов: (С1; 0) и (-С1; 0). У данного эллипса А1 = 5,
Тогда для гиперболы А = 4, С = 5, откуда

И уравнение гиперболы:
Ответ:
Составить уравнение касательной к гиперболе
Найдите вначале координаты нормали к гиперболе в точке М (если кривая задана уравнением F(X,Y) = 0, То нормаль к ней в точке М0=<Х0;у0>
Имеет координаты: П = (F′X(X0;Y0);F′Y(X0;Y0))), а затем составьте уравнение прямой, проходящей через точку М=<15; 4
Найдем координаты нормали к гиперболе в точке М.
Уравнение прямой, проходящей через точку М0(х0;у0) перпендикулярно вектору П = <A, B>, имеет вид:
Запишем уравнение касательной:
Ответ: Уравнение касательной:
Используйте определение параболы: параболой называется геометрическое место точек, для каждой из которых расстояние до фокуса равно расстоянию до директрисы.
Используем определение параболы:
Параболой называется геометрическое место точек, для каждой из которых расстояние до фокуса равно расстоянию до директрисы.
Пусть точка М(Х, У) лежит на параболе. Тогда ее расстояние до фокуса
Выразим через Х и У расстояние от точки М до директрисы.
Нормальное уравнение директрисы:
Из определения параболы DM = MF,
Ответ: уравнение параболы: Х2 + 2Ху + У2 – 6Х + 2У + 9 = 0.
Составить уравнение параболы с вершиной в начале координат, если известно, что парабола симметрична относительно оси Ох и проходит через точку А=<9; 6>. Найти координаты ее фокуса.
Из условий задачи следует, что данная парабола задается каноническим уравнением
Подставьте в это уравнение координаты точки А и найдите значение параметра Р параболы.
Из условий задачи следует, что данная парабола задается каноническим уравнением
Подставим в это уравнение координаты точки А: 36 = 2Р·9, откуда Р = 2.
Следовательно, уравнение параболы имеет вид: У2 = 4Х.
Координаты фокуса параболы задаются формулой: F=<0,5P; 0>, то есть F=<1; 0>.
Ответ: уравнение параболы: У2 = 4Х; фокус F=<1; 0>.
Кривые второго порядка
или можно встретить следующую форму записи:
К кривым второго порядка относятся окружность, эллипс, гипербола и парабола.
Покажем на примере определение значений коэффициентов.
Рассмотрим кривую второго порядка:
Вычислим определитель из коэффициентов:
Если Δ = 0, кривая второго порядка параболического типа,
если Δ > 0, кривая второго порядка эллиптического типа,




















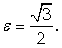






















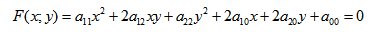
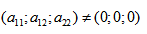
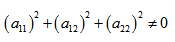
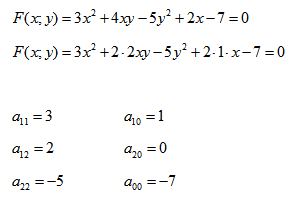
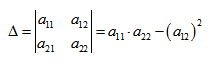
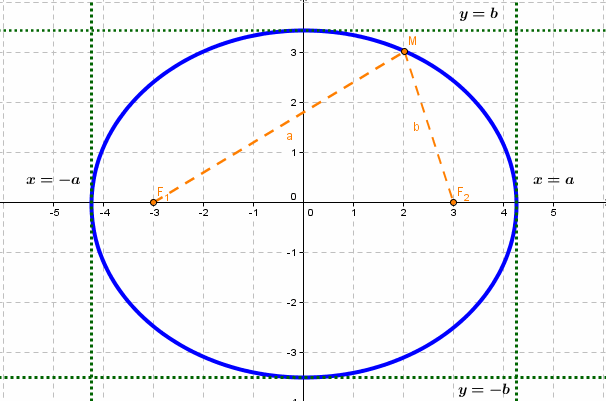
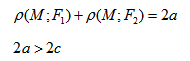


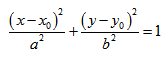
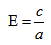
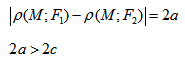

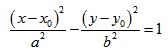
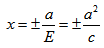
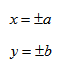
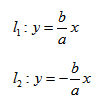
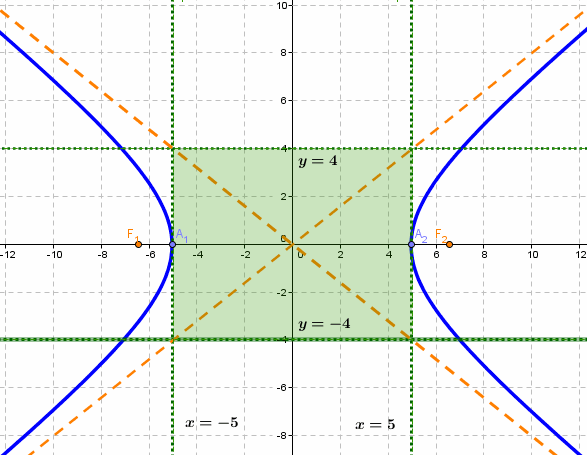
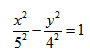
 , т.е. уравнение фигуры задает эту фигуру.
, т.е. уравнение фигуры задает эту фигуру. , есть величина постоянная (большая, чем расстояние между
, есть величина постоянная (большая, чем расстояние между  ).
). (7.5)
(7.5) координаты которой задаются формулами
координаты которой задаются формулами  будет окружность (4) переводить в эллипс, заданный соотношением
будет окружность (4) переводить в эллипс, заданный соотношением 
 называется эксцентриситетом эллипса. Эксцентриситет
называется эксцентриситетом эллипса. Эксцентриситет  характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении
характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении  становится более вытянутым
становится более вытянутым

 есть величина постоянная (не равная нулю и меньшая, чем расстояние между
есть величина постоянная (не равная нулю и меньшая, чем расстояние между  ).
).
 А расстояние
А расстояние  Подставив в формулу r=d, будем иметь
Подставив в формулу r=d, будем иметь . Возведя обе части равенства в квадрат, получим
. Возведя обе части равенства в квадрат, получим
 или
или (9.4.1)
(9.4.1) также определяют параболы.
также определяют параболы. , определяет параболу, ось симметрии которой перпендикулярна оси абсцисс; эта парабола будет восходящей, если а > 0 и нисходящей, если а
, определяет параболу, ось симметрии которой перпендикулярна оси абсцисс; эта парабола будет восходящей, если а > 0 и нисходящей, если а  О. Для этого выделим полный квадрат:
О. Для этого выделим полный квадрат:





 которое называют каноническим уравнением эллипса.
которое называют каноническим уравнением эллипса. — мень-
— мень-
 и определяет окружность радиуса а с центром в начале координат.
и определяет окружность радиуса а с центром в начале координат.
 и характеризует форму эллипса. Для окружности
и характеризует форму эллипса. Для окружности  Чем больше эксцентриситет, тем более вытянут эллипс.
Чем больше эксцентриситет, тем более вытянут эллипс.

 — каноническое уравнение эллипса с центром в точке
— каноническое уравнение эллипса с центром в точке  большей полуосью а=3 и меньшей полуосью
большей полуосью а=3 и меньшей полуосью 

 а оси
а оси  параллельны соответственно осям Ох, Оу и имеют те же направления (осуществили преобразование параллельного переноса). Тогда новые координаты точки будут равны ее старым координатам минус старые координаты нового начала, т.е.
параллельны соответственно осям Ох, Оу и имеют те же направления (осуществили преобразование параллельного переноса). Тогда новые координаты точки будут равны ее старым координатам минус старые координаты нового начала, т.е. 
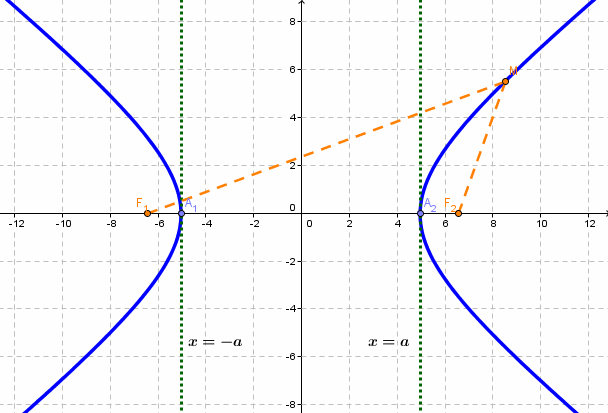
 вершин и фокусов гиперболы будут следующими:
вершин и фокусов гиперболы будут следующими:

 Задача решена.
Задача решена.