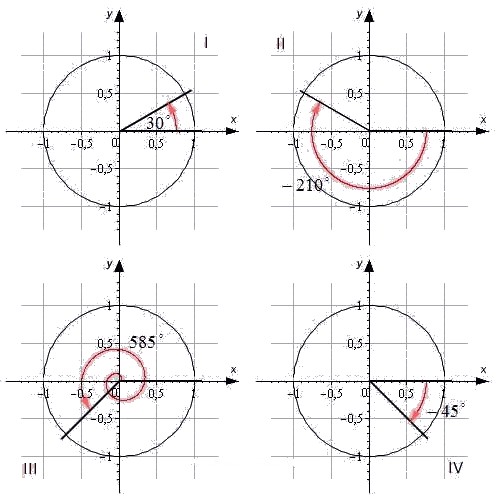
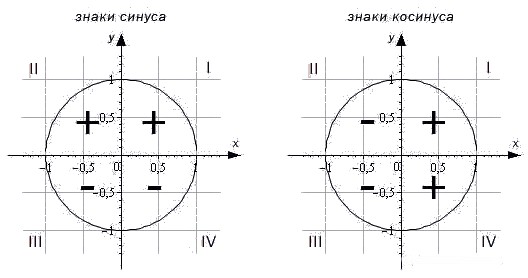
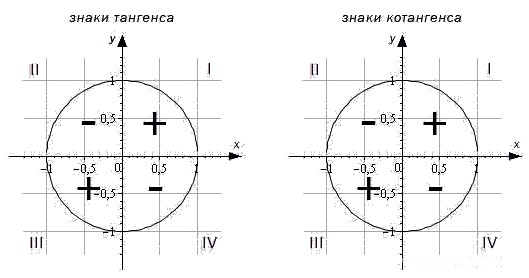
косинус в первой четверти какой знак
Тригонометрия простыми словами
Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».
Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).
Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.
Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.
Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.
Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.
Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.
Значения тригонометрических функций
для первой четверти круга (0° – 90°)
Принцип повтора знаков тригонометрических функций
Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону.
В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ.
Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно.
Тригонометрический круг
Углы в радианах
Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.
Алгебра и начала математического анализа. 10 класс
Конспект урока
Алгебра и начала математического анализа, 10 класс
Урок №31. Знаки синуса, косинуса и тангенса
Перечень вопросов, рассматриваемых в теме
1) Знаки синуса, косинуса, тангенса и котангенса;
2)Зависимость знаков синуса, косинуса, тангенса и котангенса от положения точки, движущейся по тригонометрической окружности, от произвольного угла;
3) Знаки тригонометрического выражения.
Число 
(пи) – математическая константа, которая выражает отношение длины окружности к её диаметру. Равна приблизительно 3,14.
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Какие знаки имеюткоординаты точки в зависимости от их положения в системе координат?
У точек первой четверти 
у точек второй четверти 
у точек третьей четверти 
у точек четвёртой четверти 
В какой координатной четверти находятся точки с указанными координатами
А если точка находится на тригонометрической окружности, то как узнать зависимость знака координат точки от угла поворота вокруг начала координат?
Сегодня на уроке мы узнаем знаки синуса, косинуса, тангенса и котангенса, научимся определять положение точки на тригонометрической окружности в зависимости от комбинации знаков синуса и косинуса, тангенса и котангенса.
1.Рассмотрим единичную окружность в прямоугольной системе координат хОу.
Точка Р(1;0) при повороте вокруг начала координат на угол 
переместилась в точку Рₐ. Определим её координаты.
Синусом угла
является ордината точки, полученной поворотом точки (1;0) вокруг начала координат на угол 
.
Косинусом угла
является абсцисса точки, полученной поворотом точки (1;0) вокруг начала координат на угол 
.
Если угол 
то точка Рₐ находится в первой четверти, здесь 
, значит
Если угол 
, то точка Рₐ находится в третьей четверти, здесь 
, 
, значит
, 
.
Если угол 
, то точка Рₐ находится в четвертой четверти, здесь 
, 
, значит 
, 
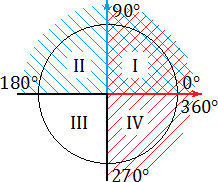
На рисунке видно какие знаки имеет синус, а какие косинус.
Примеры и разбор решения заданий тренировочного модуля
Пример1. Определить знаки синуса и косинуса угла 
.
Решение: Выясним, в какой четверти находится точка, полученная поворотом на угол 
.
во второй четверти синусы положительны, косинусы отрицательны.
Ответ: 
Пример 2. Определить знаки синуса и косинуса угла 
.
Решение: Полный угол, при котором точка «обойдёт» всю окружность, равен 
.
а это значит, что точка после 2 оборотов окажется в первой четверти, где синус и косинус положительны.
Ответ: 
Определить знаки синуса и косинуса угла 
.
Решение: Угол отрицательный, значит точка получена поворотом по часовой стрелке.
в 4 четверти синусы отрицательны, косинусы положительны.
Ответ: синус отрицательный, косинус положительный.
Определить знаки 
.
Решение: Знаем, что
, а 
. Значит, 
. Точка во второй четверти.
Ответ: 
2.Знаки тангенса и котангенса.
Тангенс это отношение синуса угла к его косинусу: 
Котангенс это отношение косинуса угла к его синусу: 
.
Тангенс и котангенс будут положительными там, где синус и косинус имеют одинаковые знаки. Это первая и третья четверти. Синус и косинус имеют разные знаки во второй и четвёртой четвертях, здесь тангенс и котангенс будут отрицательны. На рисунке изображены знаки тангенса и котангенса.
Определить знак тангенса угла 
Решение 
, угол второй четверти
Определить знак тангенса угла 
.
Решение: Угол 
в третьей четверти, тангенс положительный.
Ответ: 
Вывод: чтобы определить знаки синуса, косинуса, тангенса и котангенса, нужно:
Свойства синуса, косинуса, тангенса и котангенса
В этой статье будут рассмотрены три основных свойства тригонометрических функций: синуса, косинуса, тангенса и котангенса.
Знаки тригонометрических функций по четвертям
Часто в математическом тексте или в контексте задачи можно встретить фразу: «угол первой, второй, третьей или четвертой координатной четверти». Что это такое?
Для наглядности приведем иллюстрацию.
Теперь рассмотрим знаки, которые принимают синус, косинус, тангенс и котангенс в зависимости от того, в какой четверти лежит угол.
Свойство периодичности
При изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса данного угла остаются неизменными.
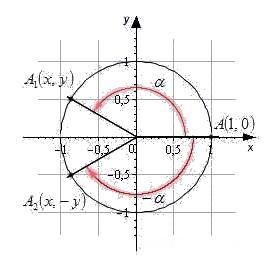
Действительно, при изменении угла на целое число оборотов мы всегда будем попадать из начальной точки A на единичной окружности в точку A 1 с одними и теми же координатами. Соответственно, не будут меняться и значения синуса, косинуса, тангенса и котангенса.
Математически данное свойство записывается так:
sin α + 2 π · z = sin α cos α + 2 π · z = cos α t g α + 2 π · z = t g α c t g α + 2 π · z = c t g α
Какое применение на практике находит это свойство? Свойство периодичности, как и формулы приведения, часто используется для вычисления значений синусов, косинусов, тангенсов и котангенсов больших углов.
sin 13 π 5 = sin 3 π 5 + 2 π = sin 3 π 5
Свойства синусов, косинусов, тангенсов и котангенсов противоположных углов
Вновь обратимся к единичной окружности.
Отсюда следует свойство синусов, косинусов, тангенсов и котангенсов противоположных углов.
Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов
Согласно этому свойству, справедливы равенства
Рассмотренное свойство часто используется при решении практических задач в случаях, когда нужно избавиться от отрицательных знаков углов в агрументах тригонометрических функций.
Знаки тригонометрических функций
Знак тригонометрической функции зависит исключительно от координатной четверти, в которой располагается числовой аргумент. В прошлый раз мы учились переводить аргументы из радианной меры в градусную (см. урок «Радианная и градусная мера угла»), а затем определять эту самую координатную четверть. Теперь займемся, собственно, определением знака синуса, косинуса и тангенса.
угла α — это ордината (координата y ) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.
угла α — это абсцисса (координата x ) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.
Все эти определения знакомы вам из курса алгебры старших классов. Однако нас интересуют не сами определения, а следствия, которые возникают на тригонометрической окружности. Взгляните:
Синим цветом обозначено положительное направление оси OY (ось ординат), красным — положительное направление оси OX (ось абсцисс). На этом «радаре» знаки тригонометрических функций становятся очевидными. В частности:
В заключение рассмотрим несколько более сложных задач. Помимо выяснения знака тригонометрической функции, здесь придется немного посчитать — именно так, как это делается в настоящих задачах B11. В принципе, это почти настоящие задачи, которые действительно встречается в ЕГЭ по математике.
Задача. Найдите sin α, если sin 2 α = 0,64 и α ∈ [π/2; π].
Поскольку sin 2 α = 0,64, имеем: sin α = ±0,8. Осталось решить: плюс или минус? По условию, угол α ∈ [π/2; π] — это II координатная четверть, где все синусы положительны. Следовательно, sin α = 0,8 — неопределенность со знаками устранена.
Задача. Найдите cos α, если cos 2 α = 0,04 и α ∈ [π; 3π/2].
Действуем аналогично, т.е. извлекаем квадратный корень: cos 2 α = 0,04 ⇒ cos α = ±0,2. По условию, угол α ∈ [π; 3π/2], т.е. речь идет о III координатной четверти. Там все косинусы отрицательны, поэтому cos α = −0,2.
Задача. Найдите sin α, если sin 2 α = 0,25 и α ∈ [3π/2; 2π].
Имеем: sin 2 α = 0,25 ⇒ sin α = ±0,5. Снова смотрим на угол: α ∈ [3π/2; 2π] — это IV координатная четверть, в которой, как известно, синус будет отрицательным. Таким образом, заключаем: sin α = −0,5.
Задача. Найдите tg α, если tg 2 α = 9 и α ∈ [0; π/2].
Все то же самое, только для тангенса. Извлекаем квадратный корень: tg 2 α = 9 ⇒ tg α = ±3. Но по условию угол α ∈ [0; π/2] — это I координатная четверть. Все тригонометрические функции, в т.ч. тангенс, там положительны, поэтому tg α = 3. Все!
Алгебра и начала математического анализа. 10 класс
Конспект урока
Алгебра и начала математического анализа, 10 класс
Урок №31. Знаки синуса, косинуса и тангенса
Перечень вопросов, рассматриваемых в теме
1) Знаки синуса, косинуса, тангенса и котангенса;
2)Зависимость знаков синуса, косинуса, тангенса и котангенса от положения точки, движущейся по тригонометрической окружности, от произвольного угла;
3) Знаки тригонометрического выражения.
Число (пи) – математическая константа, которая выражает отношение длины окружности к её диаметру. Равна приблизительно 3,14.
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Какие знаки имеюткоординаты точки в зависимости от их положения в системе координат?
У точек первой четверти
у точек второй четверти
у точек третьей четверти
у точек четвёртой четверти
В какой координатной четверти находятся точки с указанными координатами
А если точка находится на тригонометрической окружности, то как узнать зависимость знака координат точки от угла поворота вокруг начала координат?
Сегодня на уроке мы узнаем знаки синуса, косинуса, тангенса и котангенса, научимся определять положение точки на тригонометрической окружности в зависимости от комбинации знаков синуса и косинуса, тангенса и котангенса.
1.Рассмотрим единичную окружность в прямоугольной системе координат хОу.
Точка Р(1;0) при повороте вокруг начала координат на угол переместилась в точку Рₐ. Определим её координаты.
Синусом углаявляется ордината точки, полученной поворотом точки (1;0) вокруг начала координат на угол .
Косинусом углаявляется абсцисса точки, полученной поворотом точки (1;0) вокруг начала координат на угол .
Если угол то точка Рₐ находится в первой четверти, здесь , значит
Если угол , то точка Рₐ находится в третьей четверти, здесь , , значит
, .
Если угол , то точка Рₐ находится в четвертой четверти, здесь , , значит ,
На рисунке видно какие знаки имеет синус, а какие косинус.
Примеры и разбор решения заданий тренировочного модуля
Пример1. Определить знаки синуса и косинуса угла .
Решение: Выясним, в какой четверти находится точка, полученная поворотом на угол .
во второй четверти синусы положительны, косинусы отрицательны.
Ответ:
Пример 2. Определить знаки синуса и косинуса угла .
Решение: Полный угол, при котором точка «обойдёт» всю окружность, равен .
а это значит, что точка после 2 оборотов окажется в первой четверти, где синус и косинус положительны.
Ответ:
Определить знаки синуса и косинуса угла .
Решение: Угол отрицательный, значит точка получена поворотом по часовой стрелке.
в 4 четверти синусы отрицательны, косинусы положительны.
Ответ: синус отрицательный, косинус положительный.
Определить знаки .
Решение: Знаем, что, а . Значит, . Точка во второй четверти.
Ответ:
2.Знаки тангенса и котангенса.
Тангенс это отношение синуса угла к его косинусу:
Котангенс это отношение косинуса угла к его синусу: .
Тангенс и котангенс будут положительными там, где синус и косинус имеют одинаковые знаки. Это первая и третья четверти. Синус и косинус имеют разные знаки во второй и четвёртой четвертях, здесь тангенс и котангенс будут отрицательны. На рисунке изображены знаки тангенса и котангенса.
Определить знак тангенса угла
Решение , угол второй четверти
Определить знак тангенса угла .
Решение: Угол в третьей четверти, тангенс положительный.
Ответ:
Вывод: чтобы определить знаки синуса, косинуса, тангенса и котангенса, нужно: