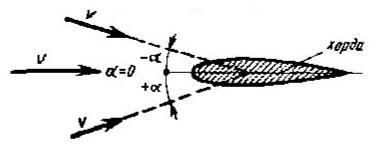
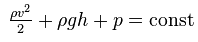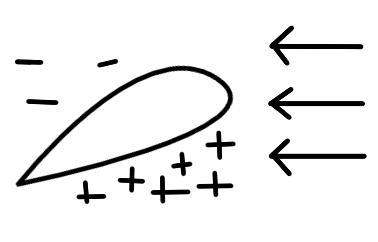какую связь в движущейся газообразной среде устанавливает основное уравнение аэродинамики

Какую связь в движущейся газообразной среде устанавливает основное уравнение аэродинамики

Вывод основного закона аэродинамики

Исторически открытие основного закона аэродинамики не состоялось, поскольку не ставилась такая задача.

Основной закон аэродинамики должен связывать все величины, действующие в аэродинамике:

1. Общее давление газа .

2. Динамическое давление газа (скоростной напор) .

3. Статическое давление газа .

Формулы, связывающей эти три величины, не было выведено.

Наиболее близко к выводу основного закона аэродинамики подошел Бернулли в 1738 году в работе «гидродинамика». В этой работе он впервые вывел уравнение, впоследствии названное его именем.

Однако это уравнение не может быть основным уравнением аэродинамики по нескольким причинам:

1. Это уравнение справедливо только для идеальной (несжимаемой) жидкости, поэтому не может быть применено для газа.

2. Это уравнение не полное. Оно составлено для двух величин из трёх, действующих в аэродинамике.

3. В правой части этого уравнения вместо физической величины стоит константа, не имеющая физического смысла.

Преобразуем уравнение Бернулли в более понятный вид.

Обычно уравнение Бернулли представляют в виде:

, (1)

Где: — константа, не имеющая физического смысла,

— динамическое давление , направленное параллельно поверхности,

— статическое давление, направленное перпендикулярно к поверхности,

— давление, направленное перпендикулярно к поверхности.

Физически последние два давления представляют собой одно статическое давление, направленное перпендикулярно к поверхности твёрдого тела:

, (2)

С учетом (2) уравнение Бернулли можно переписать более понятным образом:

, (3)

Где — давление, направленное вдоль поверхности,

— давление, направленное перпендикулярно к поверхности.

Из уравнения (1.3) следует, что сумма давлений, направленных вдоль поверхности и перпендикулярно к поверхности, постоянна.

Эта формулировка уравнения Бернулли более понятна, но не даёт физической картины процесса.

Левая часть этого уравнения имеет физический смысл. Правая часть физического смысла не имеет. Физический смысл правой части уравнения можно придать, используя молекулярно – кинетическую теорию.

Известно, что все вещества состоят из молекул. Давление газа на поверхность твёрдого тела возникает из соударения молекул газа с молекулами твёрдого тела.

Рассмотрим два случая: без движения поверхности относительно газа и с движением.

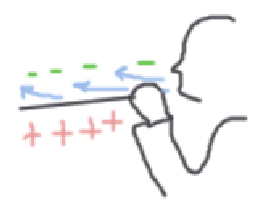
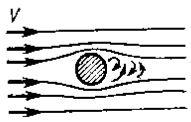
1. Давление газа на поверхность твёрдого тела без движения твердой поверхности относительно газа (рис.1.1), например, крыла самолёта, стоящего на земле.

Статическое давление газа давление газа на твёрдую поверхность является следствием давления всех молекул газа, двигающихся перпендикулярно к поверхности.

Без движения твёрдой поверхности относительно газа, справедливо основное уравнение молекулярно – кинетической теории:

, (4)

Где: — давление газа на неподвижную поверхность твёрдого тела

при возможности движения молекул по трём осям,

— коэффициент, связанный с движением молекул идеального

— количество молекул идеального газа,

— масса молекул идеального газа.

Формулу (4) можно представить также в виде

, (5)

Где: — давление газа на неподвижную поверхность твёрдого тела

при возможности движения молекул по трём осям,

— коэффициент, связанный с движением молекул идеального

— плотность идеального газа,

— квадрат средней скорости молекул идеального газа.

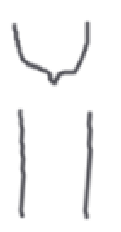
Рис. 1. При отсутствии движения твёрдой поверхности статическое давление и квадрат средней скорости молекул направлены перпендикулярно поверхности твёрдого тела.

Без движения поверхности твёрдого тела относительно газа, статическое давление, направленное перпендикулярно к поверхности, равно общему давлению газа (рис.1).

, (6)

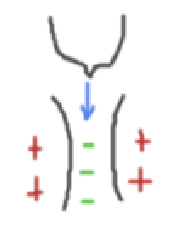
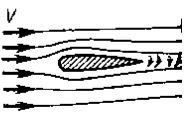
2. Давление газа на поверхность твёрдого тела при движении твёрдой поверхности относительно газа (рис. 2), например, крыла самолёта, летящего в воздухе.

При движении твёрдой поверхности относительно газа, статическое давление газа на твёрдую поверхность уменьшается. Чем больше скорость твёрдой поверхности относительно газа, тем меньше статическое давление на крыло.

Взаимосвязь статического и динамического давлений можно вывести из уравнения Бернулли (1).

Из уравнения Бернулли следует, чем больше величина динамического напора (рис.2,а), тем меньше величина статического давления .

Рис. 2. При движении твёрдой поверхности относительно газа, давление на эту поверхность уменьшается.

На (рис.2) показана физическая причина взаимосвязи статического давления и динамического напора.

Согласно уравнению Бернулли, их сумма постоянна.

Также неизменным остаётся общее давление газа , поскольку оно не зависит от того, движется в этом объёме газа самолёт или стоит на земле.

Физический механизм взаимосвязи динамического напора и статического давления достаточно простой.

Согласно молекулярно – кинетической теории, давление газа на твёрдую поверхность образуется за счет соударения молекул газа и молекул твердого тела. Движение молекул газа занимает некоторое время. При движении поверхности твёрдого тела относительно газа, молекула твёрдого тела успевает переместиться на некоторое расстояние.

Вследствие этого процесса, столкновение молекул твёрдой поверхности и газа происходит под некоторым углом к нормали, который зависит от скорости .

Чем больше скорость , тем больше этот угол, тем меньше давление на твёрдую поверхность.

Динамический напор потока определяется проекцией общего давления газа на касательную проекцию этого давления (рис. 2,а), и всегда направлен параллельно твёрдой поверхности:

, (6)

Статическое давление газа определяется проекцией общего давления на перпендикуляр. Это давление всегда направлено перпендикулярно к твердой поверхности, двигающейся со скоростью :

, (7)

Изменение величины этого давления формирует подъёмную силу крыла самолёта.

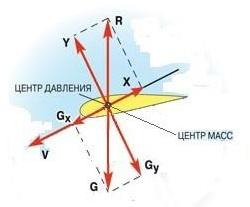
Взаимосвязь всех трёх давлений, формирующих подъёмную силу крыла самолёта можно получить с помощью теоремы Пифагора.

, (8)

Переходя к давлению, получим:

, (9)

, (10)

Учитывая (6) и (2), получим:

, (11)

Сравним с уравнением Бернулли:

,

Очевидно, что уравнение (11) более полное. В нём есть все физические величины, действующие в аэродинамике.

Таким образом, можно вывести основной закон аэродинамики:

полное давление газа при движении твёрдой поверхности относительно газа равно сумме динамического и статического давлений газа (10).

Уравнение (10) является основным законом аэродинамики. Уравнение Бернулли (1) является его частным случаем, где общее давление газа заменено константой.

Литература

1. Трофимова Т. И. Курс Физики. «Высшая школа». М.,1997.

2. Дрюков В.М. О чём молчат физики. Тула, 2004.

4. Дрюков В.М. Физика. Дополнительные материалы. Тула изд. ООО Аквариус. 2021

Источник

Какую связь в движущейся газообразной среде устанавливает основное уравнение аэродинамики

5.4. Основные законы аэродинамики

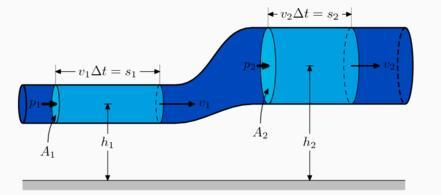
Рис. 5.14. К выводу основных уравнений аэродинамики

&nbsp&nbsp&nbspЭто соотношение называется уравнением неразрывности или уравнением постоянства расхода . При движении самолета с малыми дозвуковыми скоростями V, соответствующими числам M £ 0,4 ¸ 0,6 (конкретное значение M=V/a зависит от формы обтекаемого тела), сжимаемость воздуха практически не проявляется, т. е. можно считать, что плотность воздуха постоянна (&#961 = const). В этом случае для струйки &#961₁=&#961₂ и уравнение неразрывности примет вид

&nbsp&nbsp&nbspОтсюда следует, что для несжимаемого идеального газа скорость в струйке V тем больше, чем меньше площадь сечения струйки F, и наоборот.
&nbsp&nbsp&nbsp Уравнение Бернулли является математическим описанием закона сохранения энергии для струйки идеального сжимаемого газа:

&nbsp&nbsp&nbspт. е. внутри трубки тока, когда нет обмена массой и энергией между струйкой и окружающей ее средой (соседними струйками), сумма всех видов энергии в любом сечении струйки постоянна.
&nbsp&nbsp&nbspУчитывая только кинетическую энергию и энергию силы давления в струйке, можно записать для любого сечения струйки:

&nbsp&nbsp&nbspКинетическая энергия характеризует способность движущегося газа производить работу:

&nbsp&nbsp&nbspЭнергия силы давления характеризует способность газа производить работу силой давления, проталкивающей газ через сечение струйки:

&nbsp&nbsp&nbspОтсюда

&nbsp&nbsp&nbspС учетом этих выражений запишем уравнение Бернулли в виде

&nbsp&nbsp&nbspВ соответствии с уравнением неразрывности массовый расход m_cекdt = сonst.
&nbsp&nbsp&nbspДля идеального несжимаемого газа &#961 = сonst.
&nbsp&nbsp&nbspПоэтому для идеального несжимаемого газа уравнение Бернулли запишем в виде

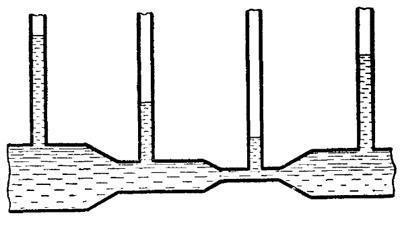
&nbsp&nbsp&nbspДля идеального несжимаемого газа сумма скоростного напора и статического давления в струйке есть величина постоянная, т. е. с увеличением скорости V давление в струйке p падает, и наоборот.

Рис. 5.15. К построению математической модели картины обтекания

Рис. 5.16. Соотношения, полученные из уравнения Бернулли при симметричном обтекании

Рис. 5.17. Соотношения, полученные из уравнения Бернулли при несимметричном обтекании

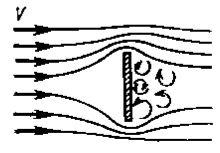
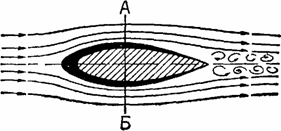
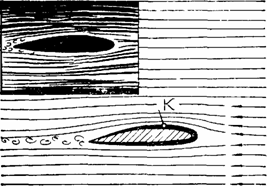
&nbsp&nbsp&nbspРаспределение скоростей &#916V_i при несимметричном обтекании профиля (рис. 5.18) сходно с распределением скоростей при вихревом движении.

Рис. 5.18. «Вихревое движение» при обтекании профиля

Рис. 5.19. Вихревая поверхность, моделирующая крыло

Источник

Основные законы аэродинамики (для несжимаемого газа).

Для облегчения изучения аэродинамических сил и явлений методом математического анализа условно заменяют реальный газ так называемым идеальным газом.

Идеальный газ – невязкий, нетеплопроводимый газ, при движении которого возникают только нормальные напряжения.

Уравнение неразрывности (Эйлер) представляет собой применение закона сохранения материи к струйке жидкости и газа.

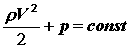
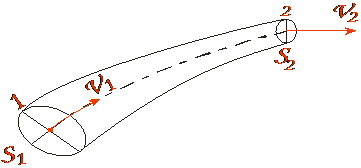По закону сохранения материи

m₁ = m₂ (масса, протекающая через сечение струйки).

Объем газа протекающего за единицу времени

S · V – секундный расход (при V малых p не изменяется),

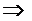а ρ₁∙ S₁ ∙ V₁ =ρ₂∙ S₂∙ V₂ – это уравнение постоянства массового массовый расход расхода или уравнение неразрывности.

Если газ несжигаем, то в формуле сократим – “ρ”

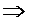получим S₁·V₁ = S₂·V₂ S·V – соnst> математическая величина закона установившегося потока.

Вывод: При установившемся течении несжимаемого газа, постоянным будет не только массовый расход, но и объёмный расход.

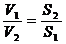Можно записать т.е. скорость в двух сечениях скорости струйки обратно пропорциональна площадям этих сечений.

Источник

Тема №1: Основные законы аэродинамики.

Основные свойства воздуха.

Атмосферой называется газовая оболочка, окружающая земной шар. Газ, составляющий эту оболочку, называется воздухом. Высота атмосферы более 2000 км. Атмосфера разделяется на тропосферу, стратосферу и ионосферу.

Тропосферой называется самый нижний слой атмосферы (7-8 км над полюсами и 16-17 км над экватором). В нём содержится около 80% массы всей атмосферы, хотя по объёму тропосфера около 1% атмосферы. Состоит тропосфера из: 78% азота, 21% кислорода и около 1% других газов. В тропосфере сосредоточен почти весь водяной пар (именно он образует облака).

Температура воздуха. Температура задаёт скорость хаотического движения молекул. Чем больше температура, тем больше скорость их движения. В тропосфере с повышением высоты уменьшается температура воздуха на 6.5° на каждые 1000м. Тёплые слои вохдуха поднимаются вверх, холодные слои опускаются вниз. Это, в совокупностью со свойствами водяного пара, приводит к образованию облаков, выпадению осадков и образованию ветров.

Градиент температур – разность температур в разных точках пространства или в разное время. К примеру, если ночью термометр показывает 15° C а днём 30° C, то градиент температур за день составляет 15°. Чем больший температурный градиент, тем большая термичность воздуха, а значит и больше и сильнее восходящие воздушные потоки. В зимнее время земля прогревается слабее и температурный градиент очень мал. Поэтому зимой более спокойная атмосфера, более пригодная дла обучения дельтапланеризму.

Давление воздуха. Давление – это сила, действующая на единицу площади перпендикулярно к ней. Всякое тело находящееся в неподвижном воздухе, испытывает со стороны последнего давление, одинаковое со всех сторон (закон Паскаля). Атмосферное давление объясняется тем, что воздух, подобно другим веществам, имеет вес и притягивается Землёй силой притяжения. Атмосферное давление уменьшается вместе с высотой. Чем больше давление, тем плотнее воздух (т.е. больше плотность воздуха). На высотах больше 5км из-за низкого давления затруднено дыхание. Многие альпинисты покоряющие вершины 7-8км гор используют кислородные баллоны со сжатым газом.

Влажность воздуха. Влажность воздуха — это количество паров воды в воздухе. Чем больше паров воды, тем выше влажность. Влажность бывает абсолютной (% воды относительно остальных газов) и относительной (% воды от максимально возможной в данных условиях). Чаще всего оперируют именно относительной влажностью. Более подробнее этот вопрос будет рассмотрен в разделе метеорология.

Инертность воздуха — свойство воздуха, характеризующее его способность сопротивляться изменениям. Чем плотнее воздух, тем сложнее его «растормошить», т. е. тем больше его инертность.

Сжимаемость воздуха. Сжимаемость — это свойство газов изменять своют плотность при изменении давления. Наибольшую значимость имеет при полётах скоростях близких или больших скорости звука.

Закон Бернулли.

Закон (уравение) Бернулли:

Возьмём трубу, через которую протекает жидкость. Наша труба не одинакова по всей длине, а имеет различный диаметр сечения (рис. 1). Закон Бернулли выражается в том, что несмотря на различный диаметр, через любое сечение в этой трубе за одно и тоже время протекает одинаковый объём жидкости.

Рис. 1. Закон Бернулли.

Т.е. сколько жидкости проходит через одно сечение трубы за некоторое время, столько же ее должно пройти за такое же время через любое другое сечение. А так как объём жидкости не изменяется, а сама жидкость практически не сжимается, то изменяется что-то другое.

Изменяется давление жидкости и её скорость. В более узкой части трубы скорость движения жидкости выше, а давление ниже. И наоборот, в широких частях трубы скорость ниже, а давление выше. Если трубу, по которой течет жидкость, снабдить впаянными в нее открытыми трубками—манометрами, то можно будет наблюдать распределение давления вдоль трубы (рис. 2).

Рис. 2. Труба разного сечения с трубками-монометрами.

Все сказанное о движении жидкости по трубам относится и к движению газа. Если скорость течения газа не слишком велика и газ не сжимается настолько, чтобы изменялся его объем, и если, кроме того, пренебречь трением, то закон Бернулли верен и для газовых потоков. В узких частях труб, где газ движется быстрее, давление его меньше, чем в широких частях.

Применительно к аэродинамике закон Бернулли выражается в том, что набегающий на крыло воздушный поток имеет различную скорость и давление под крылом и над крылом, ввиду чего возникает подъёмная сила крыла (рис. 3).

Рис. 3. Разность давлений при обтекании крыла воздушным потоком.

Проведём простой эксперимент. Возьмём небольшой листок бумаги и разместим его прямо перед собой таким образом (рис. 4):

Рис. 4. Эксперимент с листком бумаги №1

А затем подуем над его поверхностью. При это листок, вопреки ожиданиям, вместо того, чтобы прогнуться ещё больше по направлению к Земле, наоборот выпрямится (рис. 5).

Рис. 5. Результат эксперимента №1.

Можно провести и другой опыт. Возьмём 2 листка бумаги и разместим их перед собой следующим образом (рис. 6):

Рис. 6. Эксперимент с листком бумаги №2.

А затем подув в область между ними, листки бумаги, вопреки нашим ожиданиям, вместо того, чтобы отодвинуться друг от друга, наоборот приблизятся (рис. 7).

Рис. 7. Результат эксперимента №2.

Здесь мы наблюдаем тот же самый эффект. Воздушные массы с внешних сторон листком имеют большее давление, нежели ускоренный нами воздух между листками. Это и приводит к тому, что листки бумаги притягиваются к друг другу.

Этот же принцип используют для осуществления своих полётов парапланы, дельтапланы, самолёты, планёры, вертолёты и др. летательные аппараты. Именно это позволяет взлететь вверх многотонному пассажирскому самолёту.

Обтекание воздушным потоком твердых тел различной формы. Симметричное и несимметричное обтекание.

Опираясь на принципы аэродинамики инженеры смогли создать великое множество разнообразных летательных аппаратов. Некоторые из них способны нести огромный груз, с приемлемыми затратами топлива, некоторые способны разгонять скорости многократно превышающие скорости звука, некоторые способны на сложную воздушную акробатику (всевозможные манёвры высшего пилотажа вроде мёртвой петли, бочки, кобры Пугачёва и т.д.).

В общих чертах наука аэродинамика изучает обтекание тел различной формы воздушным потоком на разных скоростях и в разных условиях. Понимание общих принципов аэродинамики повышает эффективность и безопасность полётов.

При обтекании твердого тела воздушный поток подвергается деформации, что приводит к изменению скорости, давления, температуры и плотности в струйках потока. Таким образом, около поверхности обтекаемого тела создается область переменных скоростей и давлений воздуха. Изучением поведения воздушных масс в различных условиях и занимается наука аэродинамика.

От того какую форму имеет подопытный объект, будет зависеть при каких скоростях ветра он сможет летать, и насколько эффективно. К примеру, для свободного полёта человека без каких-либо приспособлений достаточно ветра силой

60-70 м\с (240 км\ч). Настолько быстрые воздушные потоки можно встретить в аэродинамических трубах. Опытные парашютисты отрабатывают в них сложные манёвры, которые в дальнейшем можно использоваться в свободном падении. От расположения рук, ног, головы зависит скорость и направление снижения.

Для начала необходимо определиться с тем, что из себя представляет набегающий поток воздуха. Воздушные массы могут самостоятельно двигаться относительно неподвижно стоящего объекта. Это ветер. Но если объект двигается относительно неподвижно стоящих воздушных масс, то мы наблюдаем тот же самый случай.

Различают два вида скоростей тела. Воздушная скорость – это скорость движения тела относительно окружающих его воздушных масс. Путевая скорость – это скорость движения тела относительно земли. Таким образом объект может иметь определённую воздушную скорость даже не сдвигаясь с места. Достаточно дождаться подходящего ветра. Действительно и обратное – объект который визуально перемещается в пространстве относительно земли, может обладать нулевой воздушной скоростью. К примеру, это может быть пушинка подхваченная и унесённая ветром.

Рассмотрим несколько типовых форм тел обтекаемых воздушным потоком.

Плоская пластинка, помещённая под углом 90° к воздушному потоку, создает довольно резкое изменение направления движения потока, обтекающего ее: торможение потока перед ней, поджатие струек у ее краев и образование непосредственно за краем пластинки разрежения и больших вихрей, которые заполняют всю область за пластинкой (рис. 8). Позади пластинки можно наблюдать хорошо заметную спутную струю. Перед пластинкой давление будет больше чем в невозмущенном потоке, а за пластинкой вследствие разрежения давление уменьшится.

Рис. 8. Спектр обтекания воздушным потоком плоской пластинки.

Такой объект называется неудобообтекаемым. Воздушный поток теряет слишком много скорости и энергии натыкаясь на него. У такого объекта очень большое лобовое сопротивление.

Если на место пластинки мы поместим шар, то картина обтекания изменится (рис. 9). Набегающий поток будет меньше тормозиться перед объектом и плавнее огибать его по краям. Однако за ним всё равно будет образовываться довольно широкая область завихрений.

Рис. 9. Спектр обтекания воздушным потоком шарообразного тела.

Наиболее плавный характер обтекания, как в передней, так и в хвостовой части, имеет каплеобразное тело (рис. 10). Деформация потока при этом незначительна, и, соответственно, в хвостовой части образуются небольшие завихрения.

Рис. 10. Спектр обтекания воздушным потоком каплеобразного тела.

Такие тела (каплеобразные) в аэродинамике называются удобообтекаемыми. Различают симметричные и несимметричные удобообтекаемые тела.

Симметричное удобообтекаемое тело создает одинаковую деформацию, поджатие воздушных струек в верхней и нижней части (сечение А-Б, рис. 11).

Рис. 11. Спектр обтекания воздушным потоком симметричного удобообтекаемого тела.

Удобообтекаемое несимметричное тело по характеру обтекания близко к удобообтекаемому симметричному, и отличается лишь величиной и разностью деформаций струек в верхней и нижней частях тела (рис. 12).

Рис. 12. Спектр обтекания воздушным потоком несимметричного удобообтекаемого тела.

Удобообтекаемые тела имеют значительно меньшее лобовое сопротивление, т.к. их форма позволяет им как можно меньше возмущать окружающие их воздушные массы. Именно такие формы придают всем внешним частям летательных аппаратов.

Чем меньше лобовое сопротивление тела, тем большую скорость оно способно развить, а соответственно и дальше улететь при прочих равных условиях.

Обтекание крыла воздушным потоком. Угол атаки. Силы, действующие на летательный аппарат.

Согласно третьему закону Ньютона сила воздействия крыла на воздух равна силе воздействия воздушного потока на крыло. Эта сила получила название полной аэродинамической силы R крыла. Так вот, в полете на дельтаплан действуют, в общем случае, только две силы: аэродинамическая сила R и сила тяжести G. Первая приложена в центре давления, а вторая — в центре массы аппарата. Для удобства представим, что две эти точки совпадают.

Если обтекание крыла имеет симметричный характер, то направление полной аэродинамической силы совпадает с направлением невозмущенного потока (рис. 13).

Рис. 13. Симметричное обтекание тела воздушным потоком.

Но в общем случае воздушный поток обтекает тело несимметрично, под каким-нибудь углом. Величина, действующей на крыло полной аэродинамической силы, зависит от угла, под которым крыло встречает набегающий поток воздуха. Этот угол называется углом атаки и определяется, как угол между хордой крыла (отрезком, соединяющим две наиболее удаленные точки крыла) и вектором скорости набегающего потока.

Угол атаки может быть положительным, отрицательным и нулевым (рис. 14):

Крыло дельтаплана имеет сложную форму, при которой хорды его сечений расположены под разными углами атаки к набегающему потоку воздуха. В этом случае, угол атаки определяется, как угол образованный так называемой средней аэродинамической хордой крыла и вектором скорости воздушного потока.

Вернемся к силам, действующим на летательный аппарат. Силы принято раскладывать по осям, а действие моментов рассматривать вокруг этих осей. Правая прямоугольная система координат — это три оси, начало которых находится в центре масс аппарата (мы для удобства совместили его с центром давления). Положительное направление оси X будет направлено по вектору скорости полета, оси Y перпендикулярно к оси X вверх, а ось Z направлена перпендикулярно к плоскости, в которой находятся оси X и Y вдоль правого крыла.

Теперь разложим полную аэродинамическую силу R и силу тяжести G по осям, направленным по траектории планирования и перпендикулярно к ней (рис. 15).

Рис. 15. Силы, действующие на крыло в полёте.

Полная аэродинамическая сила R разложится на подъемную силу Разложим силу R на подъемную силу Y, направленную перпендикулярно к пути, и силу лобового сопротивления X, направленную в противоположную сторону пути движения аппарата. Поэтому если быть математически точным, то ее надо писать со знаком «—». Слагаемые силы G — силы Gx и Gy — равны по величине и противоположны по направлению силам X и У. Надо помнить, что хотя сила Y и называется подъемной силой, но она не уравновешивает весь вес, а только одну его составляющую. Сила X уравновешивает ту составляющую силу веса, которая иногда называется маршевой силой. Маршевая сила направлена по вектору скорости поступательного движения дельтаплана или другого планера. Таким образом, движущей силой является составляющая веса Gx, возникающая вследствие движения по траектории, наклоненной к горизонту. Сила Z появляется только при криволинейном движении в горизонтальной плоскости.

Источник