какую по знаку работу совершает газ при расширении и при сжатии

Первый закон термодинамики

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.

Начнём с обсуждения работы газа.

При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).

Работа газа в изобарном процессе

Но — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:

Рис. 2. Работа газа как площадь

Итак, формула выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.

Работа газа в произвольном процессе

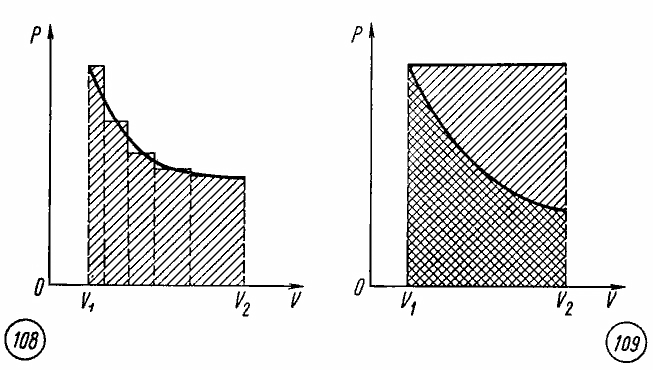
Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3 ):

Рис. 3. Работа газа как площадь

Работа, совершаемая над газом

Следовательно, работа поршня равна по модулю и противоположна по знаку работе газа:

Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.

Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.

Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.

Применение первого закона термодинамики к изопроцессам

Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.

Всё подведённое к газу тепло идёт на совершение газом работы.

Всё тепло, переданное газу, идёт на изменение его внутренней энергии.

Адиабатный процесс

Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.

Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.

Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.

В процессе адиабатного расширения газ совершает положительную работу, поэтому (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно. Именно на этом основаны методы сжижения газов.

Рис. 5. Сравнительный ход изотермы и адиабаты

В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?

При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.

А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.

Источник

Внутренняя энергия и работа идеального газа

теория по физике 🧲 термодинамика

Числом степеней свободы механической системы называют количество независимых величин, с помощью которых может быть задано положение системы.

Внутренняя энергия идеального газа представляет собой сумму только кинетической энергии всех молекул, а потенциальной энергией взаимодействия можно пренебречь:

i — степень свободы. i = 3 для одноатомного (или идеального) газа, i = 5 для двухатомного газа, i = 6 для трехатомного газа и больше.

Изменение внутренней энергии идеального газа в изопроцессах

Температура при изотермическом процессе — величина постоянная. Так как внутренняя энергия идеального газа постоянной массы в замкнутой системе зависит только от изменения температуры, то она тоже остается постоянной.

Пример №1. На рисунке показан график циклического процесса, проведенного с идеальным газом. На каком из участков внутренняя энергия газа уменьшалась?

Внутренняя энергия газа меняется только при изменении температуры. Так как она прямо пропорциональная температуре, то уменьшается она тогда, когда уменьшается и температура. Температура падает на участке 3.

Работа идеального газа

Если газ, находящийся под поршнем, нагреть, то, расширяясь, он поднимет поршень, т.е. совершит механическую работу.

Механическая работа вычисляется по формуле:

Перемещение равно разности высот поршня в конечном и начальном положении:

Также известно, что сила равна произведению давления на площадь, на которое это давление оказывается. Учтем, что направление силы и перемещения совпадают. Поэтому косинус будет равен единице. Отсюда работа идеального газа равна произведению давления на площадь поршня:

Работа идеального газа

p — давление газа, S — площадь поршня

Работа, необходимая для поднятия поршня — полезная работа. Она всегда меньше затраченной работы, которая определяется изменением внутренней энергии идеального газа при изобарном расширении:

A ‘ = p ( V 2 − V 1 ) = p Δ V > 0

Внимание! Знак работы определяется только знаком косинуса угла между направлением силы, действующей на поршень, и перемещением этого поршня.

Работа идеального газа при изобарном сжатии:

A ‘ = p ( V 2 − V 1 ) = p Δ V 0

Работа идеального газа при нагревании газа:

Внимание! В изохорном процессе работа, совершаемая газом, равна нулю, так как работа газа определяется изменением его объема. Если изменения нет, работы тоже нет.

Геометрический смысл работы в термодинамике

В термодинамике для нахождения работы можно вычислить площадь фигуры под графиком в осях (p, V).

Примеры графических задач

Изохорное охлаждение и изобарное сжатие:

Изобарное расширение:
Изобарное сжатие:
Изохорное охлаждение:
Замкнутый цикл: 1–2: A ‘ = ( p 1 − p 3 ) ( V 2 − V 1 )
Произвольный процесс:

Пример №2. На pV-диаграмме показаны два процесса, проведенные с одним и тем же количеством газообразного неона. Определите отношение работ A₂ к A₁ в этих процессах.

Неон — идеальный газ. Поэтому мы можем применять формулы, применяемые для нахождения работы идеального газа. Работа равна площади фигуры под графиком. С учетом того, что в обоих случаях изобарное расширение, получим:

A 2 = p ( V 2 − V 1 ) = 4 p ( 5 V − 3 V ) = 4 p 2 V = 8 p V

A 1 = p ( V 2 − V 1 ) = p ( 5 V − V ) = 4 p V

Видно, что работа, совершенная во втором процессе, вдвое больше работы, совершенной газом в первом процессе.

Идеальный одноатомный газ переходит из состояния 1 в состояние 2 (см. диаграмму). Масса газа не меняется. Как изменяются при этом следующие три величины: давление газа, его объём и внутренняя энергия?

Для каждой величины подберите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

Решение

На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Один моль аргона, находящийся в цилиндре при температуре T₁=600 K и давлении p₁=4⋅10 5 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p₂=10 5 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?

Источник

Презентация была опубликована 8 лет назад пользователемКирилл Чеснов

Похожие презентации

Презентация по предмету «МХК, ИЗО, Черчение» на тему: «Урок на основе интерактивного учебника. План Работа газа при расширении и сжатии. Работа газа при изобарном расширении и сжатии. Работа внешних сил при.». Скачать бесплатно и без регистрации. — Транскрипт:

1 Урок на основе интерактивного учебника

2 План Работа газа при расширении и сжатии. Работа газа при изобарном расширении и сжатии. Работа внешних сил при сжатии и расширении газа. Работа газа при изопроцессах.

3 Для перехода внутренней энергии тела в механическую работу необходимо преобра- зовать хаотическое движение его молекул в упорядоченное движение другого тела. В ка- честве такого тела целесооб- разно использовать поршень в цилиндре, перемещающий- ся под давлением газа, запол- няющего цилиндр.

4 Сила давления газа совершает работу при его расши- рении за счет изменения внутренней энергии газа. Вычислим работу, совершаемую силой давления F газа при его расширении от начального объема V 1 до конечного V 2. Будем считать, что поршень, площадь поперечного сечения которого S, перемещается на высоту h и что сила давления газа остается постоянной в процессе перемещения. h S V2V2 V1V1

7 Работа, совершаемая газом при изобарном расширении A = p ( V 2 – V 1 ) Работа газа численно равна площади фигуры под графиком р(V) p р V V1V1 V2V А = S прямоуг-ка

0) газ совершает положи- тельную работу, отдавая энергию окружающим телам. При сжатии (V» title=»При расширении (V>0) газ совершает положи- тельную работу, отдавая энергию окружающим телам. При сжатии (V» > 8 При расширении (V>0) газ совершает положи- тельную работу, отдавая энергию окружающим телам. При сжатии (V 0) газ совершает положи- тельную работу, отдавая энергию окружающим телам. При сжатии (V»> 0) газ совершает положи- тельную работу, отдавая энергию окружающим телам. При сжатии (V»> 0) газ совершает положи- тельную работу, отдавая энергию окружающим телам. При сжатии (V» title=»При расширении (V>0) газ совершает положи- тельную работу, отдавая энергию окружающим телам. При сжатии (V»>

10 Работа внешних сил при сжатии и расширении газа. Внешние силы при расширении совершают отри- цательную работу: Авн = Fhcos180°

11 Работа газа при изопроцессах. При изохорном процессе (V=0) работа газом не совершается: А = рV=0. p р2р2 V V р1р1 А = S фигуры = 0

13 При изотермическом расширении газа его давление изменяется по гиперболическому закону. Работа газа численно равна площади фигуры под изотермой и вычисляется по формуле: p 0 р1р1 р2р2 V1V1 V2V2 V 1 2.

14 Работа, совершаемая газом в процессе его расширения (или сжатия) при любом термодинамическом процессе, численно равна площади под кривой, изображающей изменение состояния газа на диаграмме р, V. p р2р2 V V р1р1 p р V V1V1 V2V А = S прямоуг-ка p 0 р1р1 р2р2 V1V1 V2V2 V 1 2

15 Вопросы для проверки усвоения нового материала: Как можно преобразовать хаотическое движение молекул газа в направленное движение макроскопического тела? Ответ. Ответ. От каких величин зависит работа, совершаемая силой давления газа? Ответ. Ответ. Какую по знаку работу совершает газ при сжатии и расширении? Ответ. Ответ.

16 Вопросы для проверки усвоения нового материала: Газ, занимающий объём V 1 и имеющий давление р 1, расширяется до объёма V 2 один раз изобарно, а другой – изотермически. В каком случае работа расширения газа больше? Обоснуйте ответ графически. Ответ. Ответ. Какое геометрическое истолкование можно дать работе на диаграмме р, V? Ответ.

17 Решите задачу: Определите работу газа, совершаемую гелием при переходе из состояния 1 в состояние 6. Ответ. Ответ. 0,1 0,3 0,5 V, м Р, кПа

18 Как можно преобразовать хаотическое движение молекул газа в направленное движение макроскопического тела? Для этого можно использовать цилиндр с поршнем. Газ, заполняющий цилиндр, при нагревании начнет расширяться и двигать поршень. Таким образом внутренняя энергия газа будет превращена в механическую энергию поршня.

19 Как можно преобразовать хаотическое движение молекул газа в направленное движение макроскопического тела? Работа газа при расширении (или сжатии) зависит от: среднего значения давления газа р от изменения объема газа V.

0.» title=»Какую по знаку работу совершает газ при сжатии и расширении? При сжатии газ совершает отрицательную работу, так какV 0.» > 20 Какую по знаку работу совершает газ при сжатии и расширении? При сжатии газ совершает отрицательную работу, так какV 0. 0.»> 0.»> 0.» title=»Какую по знаку работу совершает газ при сжатии и расширении? При сжатии газ совершает отрицательную работу, так какV 0.»>

21 Какое геометрическое истолкование можно дать работе на диаграмме р, V? Работа газа численно равна площади фигуры под кривой, изображающей изменение состояния газа на диаграмме р, V.

22 Газ, занимающий объём V 1 и имеющий давление р 1, расширяется до объёма V 2 один раз изобарно, а другой – изотермически. В каком случае работа расширения газа больше? Обоснуйте ответ графически. p р V V1V1 V2V р1р1 р2р2 V1V1 V2V2 V 1 2 Р1Р1 p Работа газа больше при изобарном расшире- нии, так как в этом случае площадь фигуры под графиком р(V) больше.

24 Полная работа гелия при переходе из состояния 1 в состояние 6 равна сумме работ газа на всех участках: А 1-6 = А 1-2 +А 2-3 +А 3-4 +А 4-5 +А 5-6 = 10 3 Дж ·10 3 Дж ·10 3 Дж = 9·10 3 Дж = 9 кДж. Ответ: 9 кДж.

Источник

Работа расширения или сжатия газа

Одним из основных термодинамических процессов, совершающихся в большинстве тепловых машин, является процесс расширения газа с совершением работы. Легко определить работу, совершаемую при изобарном расширении газа.

Если при изобарном расширении газа от объема V₁ до объема V₂ происходит перемещение поршня в цилиндре на расстояние l (рис. 7.3), то работа A’, совершенная газом, равна

, (7.27)

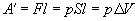
где p — давление газа, — изменение его объема.

3

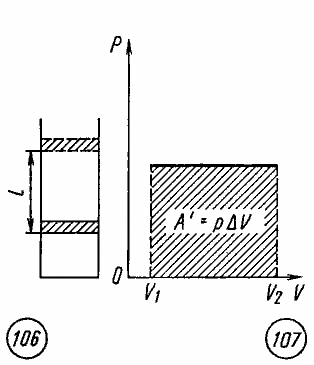
Работа при произвольном процессе расширения газа. Произвольный процесс расширения газа от объема V₁ до объема V₂ можно представить как совокупность чередующихся изобарных и изохорных процессов.

При изохорных процессах работа равна нулю, так как поршень в цилиндре не перемещается. Работа при изобарных процессах пропорциональна площади фигуры на диаграмме p, V под соответствующим участком изобары (рис. 7.5).

Следовательно, работа при произвольном процессе расширения газа прямо пропорциональна площади фигуры под соответствующим участком графика процесса на диаграмме p, V.

Работа при изотермическом расширении газа. Сравнивая площади фигур под участками изотермы и изобары (рис. 7.6), можно сделать вывод, что расширение газа от объема V₁ до объема V₂ при одинаковом начальном значении давления газа сопровождается в случае изобарного расширения совершением большей работы.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

Какую по знаку работу совершает газ при расширении и при сжатии

Идеальный газ совершил работу 300 Дж и при этом внутренняя энергия газа увеличилась на 300 Дж. Какое количество теплоты отдал или получил газ в этом процессе?

Согласно первому началу термодинамики, тепло, переданное системе, идет на изменение внутренней энергии и совершение работы против внешних сил: Следовательно, газ получил количество теплоты:

Если идеальный газ совершил работу 300 Дж и при этом внутренняя энергия газа уменьшилась на 300 Дж, то газ в этом процессе

4) не отдал и не получил теплоту

Согласно первому началу термодинамики, тепло, переданное системе, идёт на изменение внутренней энергии и совершение работы против внешних сил: Следовательно, газ получил количество теплоты:

Таким образом, газ не отдал и не получил теплоты.

Постоянную массу газа в сосуде сжали, совершив работу 30 Дж. Внутренняя энергия газа при этом увеличилась на 25 Дж. Следовательно, газ

1) получил извне количество теплоты, равное 5 Дж

2) отдал окружающей среде количество теплоты, равное 5 Дж

3) получил извне количество теплоты, равное 55 Дж

4) отдал окружающей среде количество теплоты, равное 55 Дж

Согласно первому началу термодинамики, внутреннюю энергию системы можно изменить, передав системе тепло или совершив над ней работу:

Следовательно, газ получил теплоту

Таким образом, газ отдал окружающей среде количество теплоты, равное 5 Дж.

А ПОЧЕМУ РАБОТУ ОТНИМАЛИ А НЕ ПИБАВЛЯЛИ КАК ПО ФОРМУЛЕ.

На сколько я понял из Вашего вопроса, Вас интересует, почему первое начало термодинамики выписано так, как оно выписано. Прокомментирую.

Существует два способа записи закона сохранения энергии (первого начала) в термодинамике для квазистатических процессов (протекающих достаточно медленно, так что можно считать, что в любой момент времени система находится в состоянии равновесия). Они звучат следующим образом.

1) Внутреннюю энергию системы можно изменить, передав ему тепло или совершив над ним работу:

.

Обратите внимание, здесь под понимается работа внешних сил над газом: если, например, газ сжимается, то внешние силы совершают над ним положительную работу, ежели он расширяется, то внешние силы совершают отрицательную работу (так как направление действия внешних сил и перемещение стенки сосуда направлены противоположно).

2) Для квазистатических процессов внутреннее давление газа сравнивается с внешним, поэтому работа газа против внешних сил равна по величине и противоположна по знаку работе внешних сил: (при расширении газ совершает положительную работу, при сжатии — отрицательную). Поэтому можно переписать первое начало в следующем виде:

.

Словами это звучит следующим образом: «переданное системе тепло идет на изменение ее внутренней энергии и на совершении работы против внешних сил».

В разных задачах удобно пользоваться разными записями первого начала. Чтобы не путаться в знаках, мой Вам совет: лучше запоминайте не формулы, а тот физический смысл, который за ними кроется (то есть запомните лучше словесные описания).

Алексей, ваши старания достойны уважения, но боюсь в данном случае уже ничего нельзя сделать.

Источник