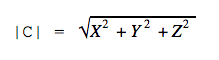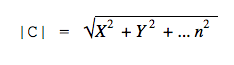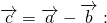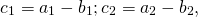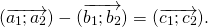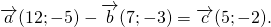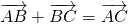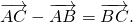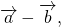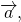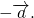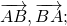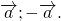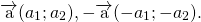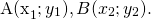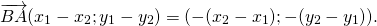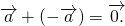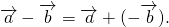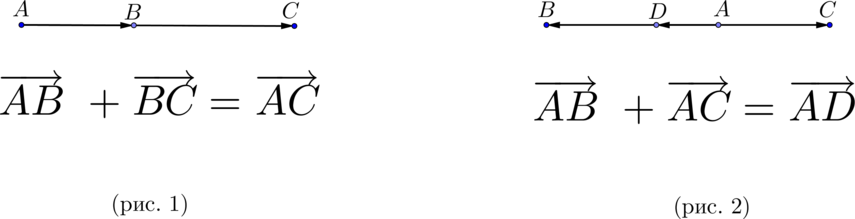какую фигуру образуют вектора при вычитании

Операции с векторами

Как сложить и перемножить векторы (и зачем).

Мы постепенно показываем вам математику за пределами школьной программы. Начинали со знакомства с векторами, теперь сделаем следующий шаг.

Напомним основные мысли:

С векторами можно совершать некоторые математические операции. Вот о них и поговорим.

Правильно — векторы

Математики часто говорят во множественном числе «вектора», но по словарю правильно «векторы». Это такой профессиональный жаргон, как «договора», «бухгалтера» и «сервера». Мы будем использовать «векторы», но если вы окажетесь в постковидном математическом баре, лучше говорите «вектора».

Сложение

Представим четыре вектора, которые лежат в двухмерном пространстве и пока что не связаны между собой. Нарисуем эти векторы и обозначим их буквами X, Y, Z, K.

Поскольку векторы находятся в одном пространстве, координаты каждого состоят из одинакового количества чисел. У нас пример с двухмерным пространством и два числа. Выглядеть это будет так: X = (6, 4); Y = (3, −2); Z = (−7, −5); K = (−10, 4).

Векторы X, Y, Z, K в двухмерном пространстве

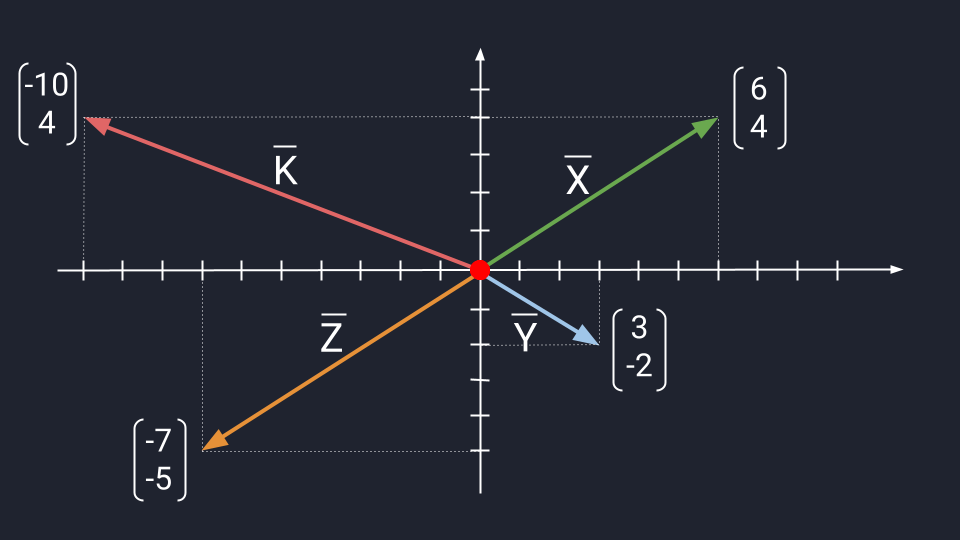
Если у нас несколько векторов с одинаковым количеством чисел, то эти числа можно поэлементно складывать. Для этого мы берём первое число одного вектора, складываем его с первым числом другого вектора и так далее.

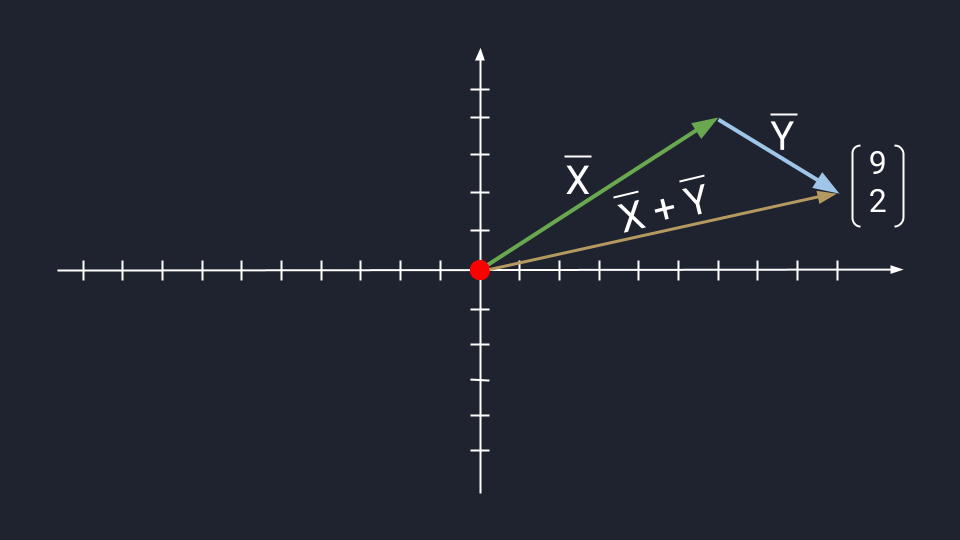
Предположим, нам нужно сложить векторы X и Y.

X = (6, 4)
Y = (3, −2)
X + Y = (9, 2)

Вроде просто: складываешь последовательно все координаты, результаты сложения складываешь в исходные коробочки. Так можно делать с любым количеством координат. Помните, что вектор — это необязательно стрелка в двумерном пространстве. Она может быть и в десятимерном пространстве — с точки зрения математики это неважно.

Например, вот сложение векторов с пятью координатами:

Интуитивное изображение сложения

Для интуитивного восприятия удобно использовать векторы с двумя координатами. Их удобно рисовать на координатной плоскости и таким образом смотреть на геометрию.

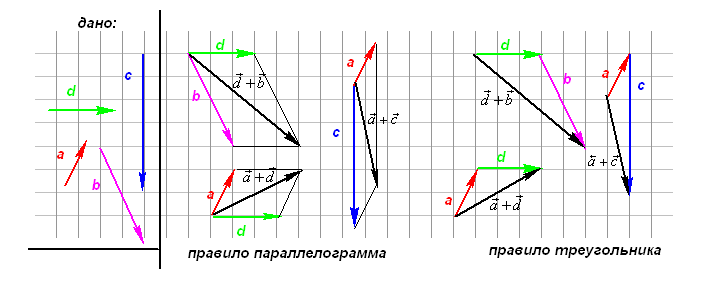
Например, можно на плоскости показать, как будет работать сложение двух векторов. Для этого есть два метода: метод треугольника и метод параллелограмма.

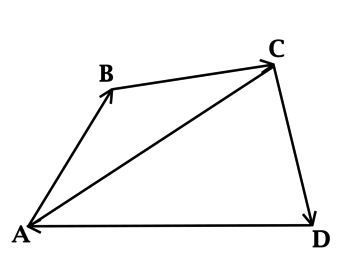
Метод треугольника: ставим векторы Х и Y в очередь друг за другом. Для этого берём вектор Х, ставим за ним вектор Y и получаем новый вектор. Новый вектор начинается в хвосте вектора Х и заканчивается на стрелке вектора Y. Этот вектор — результат сложения. Представьте, что это ребёночек двух векторов.

Сложение векторов по методу треугольника: X = (6, 4); Y = (3, −2); Х + Y = (9, 2)

Чтобы воспользоваться методом параллелограмма, нам нужно поставить векторы Х и Y в одну исходную точку. Дальше мы дублируем векторы Х и Y, формируем параллелограмм и получаем новый вектор. В новом векторе соединяем исходную точку с исходной точкой дублирующих векторов — стрелка проходит посередине параллелограмма. Длина нового вектора — это сумма векторов Х и Y.

Сложение по методу параллелограмма и треугольника даёт одинаковый результат. Поэтому выбирайте вариант, который больше подходит под задачу.

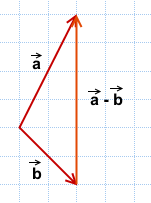
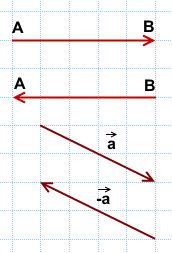
Вычитание

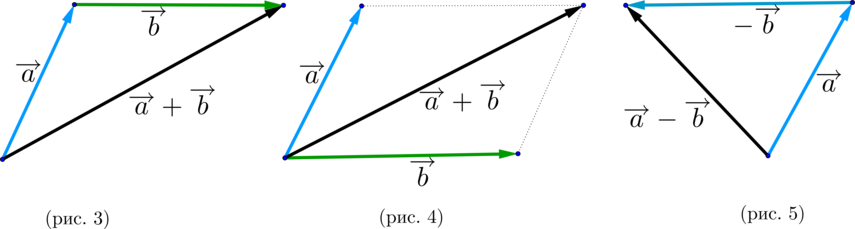
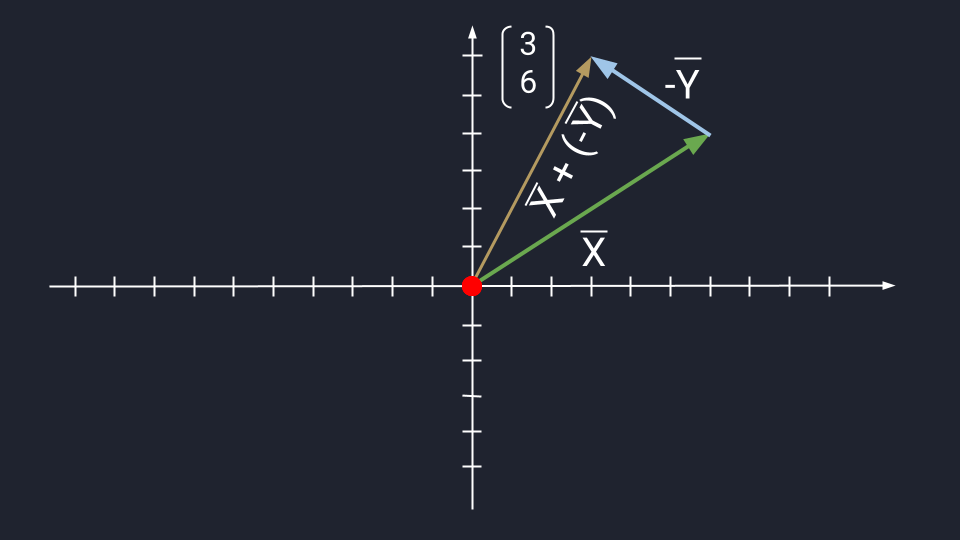
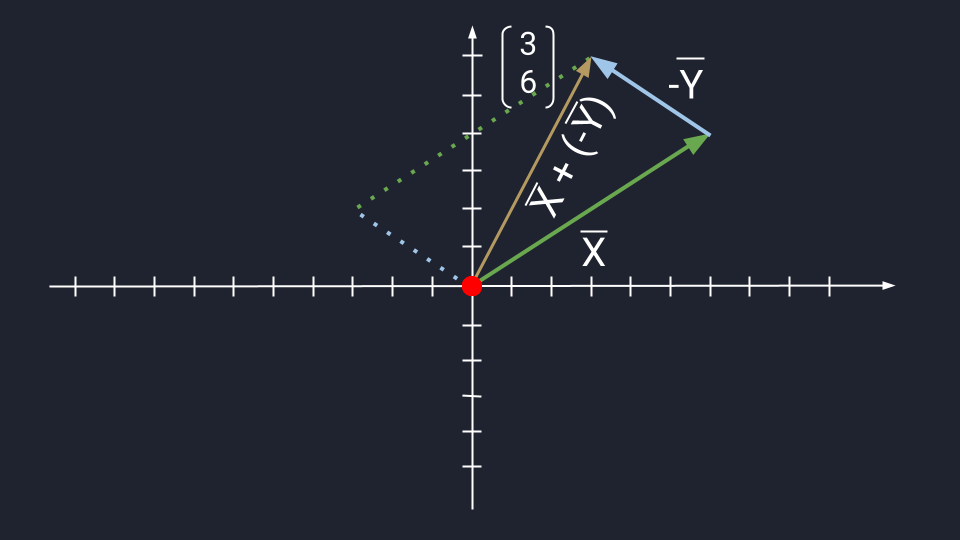
Вычитание векторов немного сложнее. Чтобы вычесть векторы, нужно «развернуть» вычитаемый вектор и сложить его с исходным. «Развернуть» — то есть направить в обратную сторону, «перевернув» знаки координат. Получится конструкция вроде такой: Х + (−Y)

Дальше используются правила сложения. Пошагово это выглядит так:

Теперь посмотрим, как выглядит вычитание векторов на графике:

Вычитание векторов по методу треугольника: X = (6, 4); −Y = (−3, 2); X + (−Y) = (3, 6) Вычитание векторов по методу параллелограмма: X = (6, 4); −Y = (−3, 2); X + (−Y) = (3, 6)

Длина вектора

Длина вектора — это одно число, которое измеряется расстоянием от кончика до стрелки вектора. Длину вектора нельзя путать с координатами. Координаты — это несколько чисел, которые указывают на расположение стрелки вектора. По координатам можно определить только конечную точку вектора. Например, если X = (6, 2), то стрелка будет находиться в точке 6 по оси Х. Или другой пример: если Y = (6, 5), то стрелка этого вектора будет находиться в точке 5 по оси Y.

Предположим, нам известны начальные точки векторов X и Y. Пусть это будет точка 2 по оси X и точка 2 по оси Y. Так мы можем легко посчитать длину отрезков:

X = 6 − 2 = 4
Y = 5 − 2 = 3

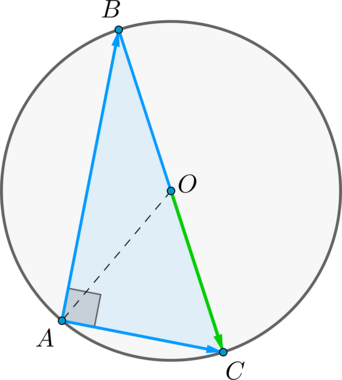
Иногда приходится рассчитывать длину третьего вектора, который привязан к двум другим векторам. Это легко сделать с помощью теоремы Пифагора — это когда квадрат гипотенузы равен сумме квадратов катетов. В нашем случае катетами будут длины векторов X и Y. Вспоминаем школьную формулу и считаем:

|C|2 = 42 + 32 = 25
|C| = √25 = 5 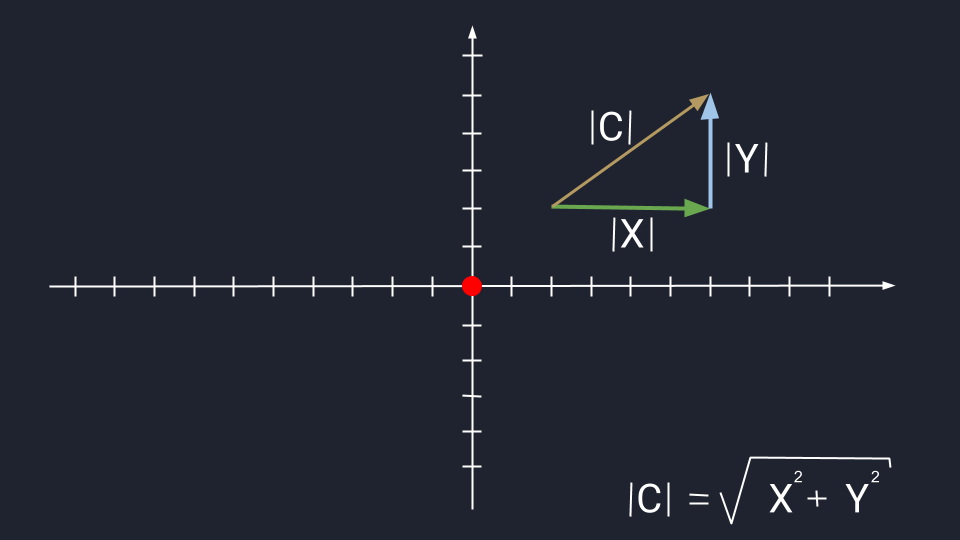Длина вектора считается по формуле прямоугольного треугольника. Чтобы было проще представить — перенесите векторы на систему координат

Это формула для двумерного пространства. В трёхмерном пространстве формула похожая: нужно сложить квадраты трёх координат и вычислить квадратный корень из суммы.

В пространстве с большим числом измерений формула выглядит сложнее, но по сути то же: складываем все квадраты координат и получаем квадратный корень из этой суммы.

Умножение и деление вектора на число

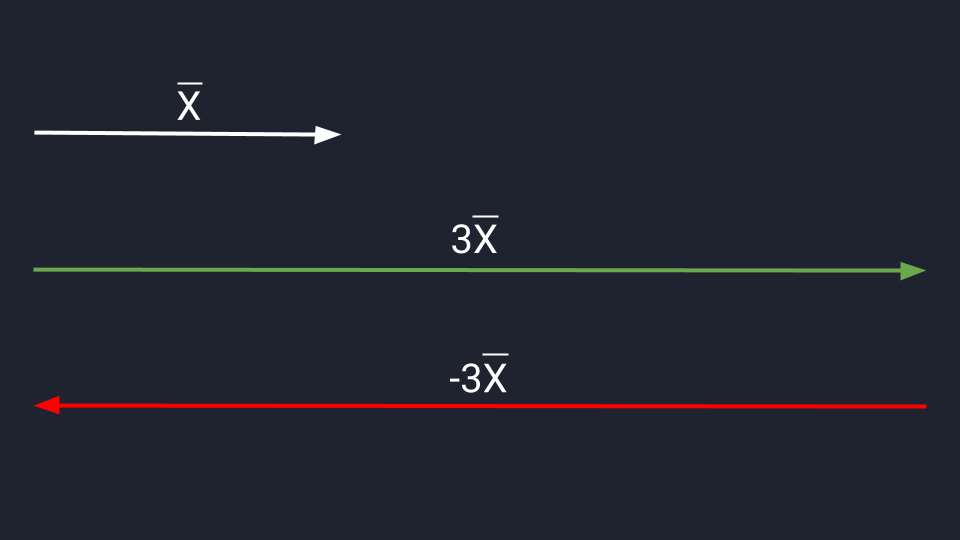
Умножение и деление позволяют изменить длину и направление вектора. Если мы умножим вектор Х на три, то увеличим его длину в три раза. Если умножим на минус три — увеличим длину и изменим его направление на противоположное.

Умножение вектора на число

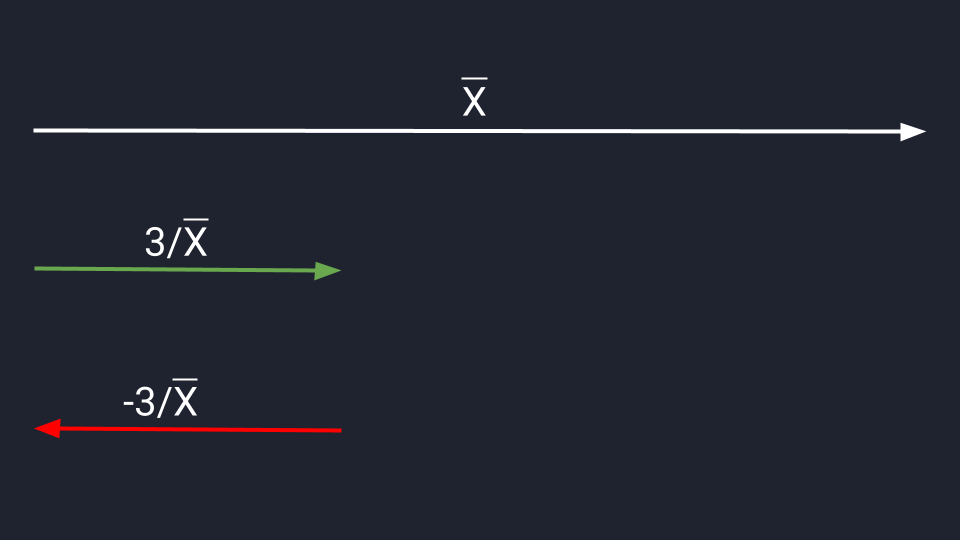
Для деления сохраняются аналогичные правила. Делим вектор Х на три и сокращаем длину в три раза. Делим на минус три — сокращаем и разворачиваем.

Деление вектора на число

Да вроде несложно!

Пока ничего сложного. Но если углубляться, вы узнаете, что:

Что дальше

В следующей статье рассмотрим линейную зависимость векторов. Чтобы не скучать — посмотрите интервью с Анастасией Никулиной. Анастасия сеньор-дата-сайентист в Росбанке и по совместительству блогер с интересной историей.

Источник

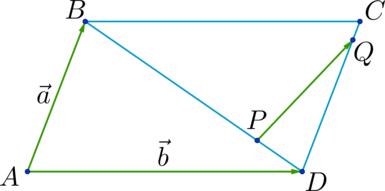
Разность векторов

Разность векторов

— это такой вектор

который в сумме с вектором b даёт вектор a:

На основе определения находим координаты вектора

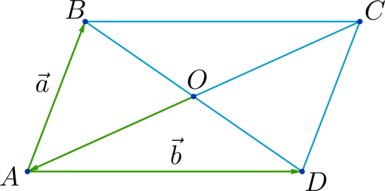
Как построить разность двух векторов?

Из равенства

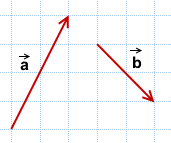
правило построения разности двух векторов

Чтобы построить вектор, равный разности векторов

надо отложить оба вектора от одной точки. Разность векторов — вектор, проведённый от конца вычитаемого b к концу уменьшаемого a.

Противоположные векторы — это противоположно направленные векторы одинаковой длины.

Вектор, противоположный вектору

Примеры противоположных векторов:

Свойства противоположных векторов:

1) Противоположные векторы имеют противоположные координаты:

2) Сумма противоположных векторов равна нулевому вектору:

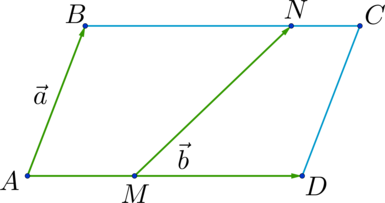
2 способ построения разности векторов

Чтобы построить разность векторов

можно к вектору a прибавить вектор, противоположный вектору b:

То есть вычитание векторов заменяем сложением уменьшаемого с вектором, противоположным вычитаемому.

Источник

Сложение и вычитание векторов

Существование: Имеем два следующих случая:

Из данного выше построения сразу же будет следовать единственность данного вектора.

Сумма векторов. Сложение векторов. Правило треугольника

Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.

Такая операция выполняется по правилу многоугольника.

Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
\( \vec + \vec = \left( <+ , + , + > \right) \)

Отметим несколько свойств сложения двух векторов:

Для произвольного вектора \( \overrightarrow \) выполняется равенство

Для произвольных точек \( A,\ B\ и\ C \) справедливо следующее равенство

Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.

Разность векторов. Вычитание векторов

Длина нулевого вектора равна нулю:
\( \left| \vec <0>\right| = 0 \)

Умножение вектора на число

Определение Произведением вектора \( \overrightarrow \) на действительное число \( k \) называется вектор \( \overrightarrow \) удовлетворяющий следующим условиям:

Длина вектора \( \overrightarrow \) равна \( \left|\overrightarrow\right|=\left|k\right||\overrightarrow| \) ;

Векторы \( \overrightarrow \) и \( \overrightarrow \) сонаправлены, при \( k\ge 0 \) и противоположно направлены, если \( k\le 0 \)

Источник

Векторы: правила сложения и вычитания

Вектор \(\overrightarrow\) можно рассматривать как перемещение точки из положения \(A\) (начало движения) в положение \(B\) (конец движения). То есть траектория движения в этом случае не важна, важны только начало и конец!

\(\blacktriangleright\) Два вектора коллинеарны, если они лежат на одной прямой или на двух параллельных прямых.
В противном случае векторы называются неколлинеарными.

\(\blacktriangleright\) Два коллинеарных вектора называются сонаправленными, если их направления совпадают.
Если их направления противоположны, то они называются противоположно направленными.

Правила сложения коллинеарных векторов:

\(\blacktriangleright\) Для того, чтобы сложить два сонаправленных вектора, можно отложить второй вектор от конца первого. Тогда их сумма – вектор, начало которого совпадает с началом первого вектора, а конец – с концом второго (рис. 1).

\(\blacktriangleright\) Для того, чтобы сложить два противоположно направленных вектора, можно отложить второй вектор от начала первого. Тогда их сумма – вектор, начало которого совпадает с началом обоих векторов, длина равна разности длин векторов, направление совпадает с направлением большего по длине вектора (рис. 2).

Правила сложения неколлинеарных векторов \(\overrightarrow \) и \(\overrightarrow\) :

\(\blacktriangleright\) Правило треугольника (рис. 3).

\(\blacktriangleright\) Правило параллелограмма (рис. 4).

\[\begin \overrightarrow = \overrightarrow + \overrightarrow = \frac<1><5>\overrightarrow + \frac<9><10>\overrightarrow = \frac<1><5>(\overrightarrow + \overrightarrow) + \frac<9><10>\overrightarrow =\\ = \frac<1><5>(\overrightarrow + \overrightarrow) + \frac<9><10>\overrightarrow = \frac<1><5>(\overrightarrow — \overrightarrow) + \frac<9><10>\overrightarrow = \frac<1><5>\overrightarrow + \frac<7><10>\overrightarrow = \frac<1><5>\vec + \frac<7><10>\vec\end\]

Старшеклассники, которые готовятся к сдаче ЕГЭ по математике и при этом рассчитывают на получение достойных баллов, обязательно должны повторить тему «Правила сложения и вычитания нескольких векторов». Как видно из многолетней практики, подобные задания каждый год включаются в аттестационное испытание. Если у выпускника вызывают трудности задачи из раздела «Геометрия на плоскости», к примеру, в которых требуется применить правила сложения и вычитания векторов, ему обязательно стоит повторить или вновь разобраться в материале, чтобы успешно сдать ЕГЭ.

Образовательный проект «Школково» предлагает новый подход в подготовке к аттестационному испытанию. Наш ресурс выстроен таким образом, чтобы учащиеся смогли выявить наиболее сложные для себя разделы и восполнить пробелы в знаниях. Специалисты «Школково» подготовили и систематизировали весь необходимый материал для подготовки к сдаче аттестационного испытания.

Для того чтобы задачи ЕГЭ, в которых необходимо применить правила сложения и вычитания двух векторов, не вызывали затруднений, мы рекомендуем прежде всего освежить в памяти базовые понятия. Найти этот материал учащиеся смогут в разделе «Теоретическая справка».

Если вы уже вспомнили правило вычитания векторов и основные определения по данной теме, предлагаем закрепить полученные знания, выполнив соответствующие упражнения, которые подобрали специалисты образовательного портала «Школково». Для каждой задачи на сайте представлен алгоритм решения и дан правильный ответ. В теме «Правила сложения векторов» представлены различные упражнения; выполнив два-три сравнительно легких задания, учащиеся могут последовательно переходить к более сложным.

Оттачивать собственные навыки по таким, например, заданиям, как задачи на координатной плоскости, школьники имеют возможность в режиме онлайн, находясь в Москве или любом другом городе России. При необходимости задание можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.

Источник

Физика

Тестирование онлайн

Вектор

Если начало вектора совпадает с его концом, получим нулевой вектор.

Два вектора являются равными, если их длина одинаковая и они имеют одинаковое направление. Они совмещаются при переносе.

На рисунке только вектор a равен вектору b. Вектор c им не равен, так как направлен в противоположную сторону

Проекция вектора

Спроецируем вектор перемещения на ось Ox и на ось Oy. Для того, чтобы получить проекцию необходимо из координаты конца вектора отнять координату начала. На ось ОХ: s_x=x-x₀, на ось ОУ: s_y=y-y₀.

Частные случаи, когда проекция на ось Ox или Oy нулевая.

Сумма составляющих вектора по осям равна данному вектору, т.е.

Сложение векторов

Правило треугольника: от конца первого вектора отложить второй вектор, тогда их суммой будет вектор, начало которого совпадает с началом первого вектора, а конец с концом второго вектора.

Рассмотрим правила на примерах.

Вычитание векторов

Упражнения

Может ли при сложении двух векторов по правилу параллелограмма равнодействующая быть численно равной одному из составляющих векторов?

Может ли при сложении двух векторов по правилу параллелограмма равнодействующая быть меньше меньшего из составляющих векторов?

Источник